Greenplum vs Citus. Part 2
In the previous article, we have discussed the fundamental architectural features of Citus. We have also deeply analyzed several specifics of planning and query execution.
In the second part, we will talk about the shard rebalancing — it is of special interest to us due to our Greengage project plans, where we’re going to solve the cluster downscaling problem (a.k.a. ggshrink — reducing the number of segments and redistributing the data among a lesser number of segments).
In the final part of this article, we will compare Citus and Greenplum using the TPC-DS tests and discuss the results.
Rebalance
The Citus architecture allows various approaches when it comes to implementing the data distribution and load balancing mechanisms.
The Citus' usage scenarios are such that data skew isn’t unheard of. For example, when certain users' data is mapped to shards (we have discussed the approach with the multi-tenant architecture in the first part), it’s quite problematic to get an even distribution that is more common for Greenplum. Some shards will occupy more space since they receive a larger amount of data and possibly a higher load. The Citus developers obviously had to consider such peculiarities in the approach to solve the load balancing problem under such initial conditions.
In my opinion, such requirements have led to Citus offering quite interesting possible configurations of the data distribution:
-
basic algorithms use such terms as
costandcapacitywhich allows implementing various balancing strategies; -
the
by_shard_countandby_disk_sizebuilt-in balancing strategies might cover most of the casual use cases; -
those who need something outside of the built-in algorithms framework can implement their own
costandcapacitycomputation functions, thereby tweaking the algorithm to their data and load distribution needs.
The basic concepts of rebalancing are shards, shard group, shard group placement, and node group.
A shard group contains a set of shards with the same key range.
A shard group placement is a mapping of a shard group to a node group, where a node group is identified by some integer identifier — groupid (can be found in the pg_dist_node table).
Moving shards between nodes means moving the whole group of shards. Such necessity becomes obvious if we remind ourselves about the co-location property of shards that exists for Citus to effectively join tables.
Before we look at the rebalancing algorithm, I suggest we consider the following:
-
the definition of
costandcapacityin terms of shards and nodes for their placement; -
the definition of the node’s
utilizationwhen placing a shard group; -
the definition of a possibility of placing a shard group on a node (so-called
disallowedPlacementList); -
assumptions and limitations that we considered by the developers when solving the rebalancing problem.
Cost is an estimated property of a shard group that allows comparing shard groups for balancing.
For example, for the by_disk_size strategy this value is equal to the occupied disk space, however, the user can define this value by a custom property (by implementing a custom function and matching it with a custom strategy).
Capacity is a node property that receives a shard group. The semantics of the default value is equal to 1 since the contribution of each node is considered to be the same. The user can redefine this value at will if some nodes contribute more than others (e.g. a cluster was expanded with some more powerful nodes).
The utilization connects cost and capacity as follows:
where is utilization of the i-th node, is cost of the j-th group, is capacity of the i-th node.
The possibility of a group placement concept is necessary for implementing strategies of mapping shard groups to certain nodes.
The first and most important assumption is that the algorithm isn’t looking for the ideal solution of the balancing problem, but is rather satisfied with a somewhat locally optimal placement of shard groups. The architecture documentation provides a link to the theoretical basis of this and similar problems, but here we are more interested in the practical side. What does a locally optimal placement mean? Consider the following shard groups:
SELECT
shardid,
table_name,
shard_size,
shard_size >> 20 AS "shard_size_in_MiB",
nodename,
nodeport
FROM citus_shards as s
WHERE table_name = 'dist_table'::regclass
ORDER BY nodename, nodeport;shardid | table_name | shard_size | shard_size_in_MiB | nodename | nodeport ---------+------------+------------+-------------------+-----------+---------- 102490 | dist_table | 253837312 | 242 | citus-db1 | 8002 102492 | dist_table | 417579008 | 398 | citus-db1 | 8002 102491 | dist_table | 491520 | 0 | citus-db2 | 8003 102493 | dist_table | 73728 | 0 | citus-db2 | 8003 (4 rows)
As shown in the table above, the utilization of the citus-db1 and citus-db2 differs by 3 orders of magnitude.
SELECT
nodename,
nodeport,
norm_node_utilization_for_table('dist_table'::regclass) as node_utilization
FROM citus_shards AS s
WHERE table_name = 'dist_table'::regclass
GROUP BY nodename, nodeport;nodename | nodeport | node_utilization -----------+----------+------------------ citus-db1 | 8002 | 1.998 citus-db2 | 8003 | 0.001 (2 rows)
The by_disk_size default strategy considers the shard size in bytes as the cost value, which can be hard to interpret with a considerable skew. To demonstrate such skew I have used the norm_node_utilization_for_table custom function for some value normalization.
This value is computed as "how many times the data on shards is greater/less that some ideal mean value that is based on the number of nodes and the total amount of data".
Also it’s worth noting that the cost of each shard is incremented by the citus.rebalancer_by_disk_size_base_cost value which is by default equal to 104857600 bytes. It’s done in order to avoid the faulty balancing of the empty shards or those with little amount of data. For testing and transparency, I’ve set this value to 0.
Thus, for my test cluster of 2 nodes and 4 shards, the total cost is 671981568 bytes while the total capacity is 2.
A crucial part of the correct rebalancing is limiting values, which prevent the redundant movements, since the algorithm doesn’t account for the cost of movements. That is, if to reach a balance from a 10 GB imbalance it needs to move TB of data, it will happily plan such a movement. We can say that without the limiting values, the goal to balance a cluster always justifies the means. In a sense these values represent a range of the node utilization, in which a node is considered balanced (threshold). In this case, the range is (369589856, 302391712), which is around 10% of the mean utilization of the two nodes. So, if a value is inside this range, the node is balanced.
There is also a second threshold value — improvement_threshold. To demonstrate the necessity of this limitation, the documentation gives the following example: consider two nodes — A=200GB and B=99GB. Moving 100 GB of shard data from A to B would improve their placement in terms of balance (A=100GB, B=199GB), but the actual profit of such movement is questionable, considering the resources needed for the operation (remember, the algorithm doesn’t account for the movement costs!). The value of this threshold is set to 50%. The idea is to estimate how profitable the data movement is in terms of node utilization. If the utilization value improves by more than 50%, the movement is planned.
Rebalancing algorithm
Citus allows us to get a query plan without an actual shard redistribution by calling get_rebalance_table_shards_plan. This function is based on the rebalance algorithm implementation, which allows us to delve into it on the example of calling it for my cluster of 2 nodes and a table of 4 shards.
The initial shard state:
shardid | table_name | shard_size | shard_size_in_MiB | nodename | nodeport ---------+------------+------------+-------------------+-----------+---------- 102490 | dist_table | 253837312 | 242 | citus-db1 | 8002 102492 | dist_table | 417579008 | 398 | citus-db1 | 8002 102491 | dist_table | 491520 | 0 | citus-db2 | 8003 102493 | dist_table | 73728 | 0 | citus-db2 | 8003
So, in practice, the algorithm works as follows:
-
Determination of the rebalance strategy and other input parameters (thresholds, the
drainOnlyflag of the node release). In my case, thethresholdvalue is the default 0.1 (i.e. 10%);improvement_threshold = 0.5(i.e. 50%). -
Formation of the active node list (worker nodes that can receive the
SELECTrequests, except the coordinator) and sorting it by hostname and port. In my case, it’s 3 active nodes (2 worker nodes and a coordinator) and 4 possible shard placements. -
Iteration over a list of tables, for which a balancing is needed, where each table gets a list of possible shard placements. I chose one table for balancing —
dist_table. There are no special limitations for balancing, all nodes are active, hence the number of possible shard placements is 4. -
To get a list of active nodes, list of possible shard group placements and parameters for the first step, a step-by-step plan for moving shard groups between nodes that lead to a balanced cluster is formed:
-
Initialization of the shard placement list in terms of the upcoming shard movement plan (
shardPlacementList):-
Computation of the node capacity value (
capacity). For the coordinator, the default capacity is 0, for the worker nodes — 1. -
A total capacity is computed (
totalCapacity). In my case, it’s 2. -
Computation of the shard cost (
cost) based on their current placement. Values of theshard_sizecolumn. -
Computation of the shard utilization (
utilization) for the current placement on a node. For thecapacityandcostcomputation functions the default value equals the cost for each shard (i.e. the shard size) sincecapacityis 1. -
A total cost is computed for all shards (
totalCost). It’s equal toSUM(shard_size) = 671981568. -
A shard list is sorted in the descending and ascending order by utilization or node capacity. .
-
-
Planning the movement of shards from the nodes on which the shards aren’t allowed to exist (
disallowedPlacementList). In my case, there are no such shards. -
Taking into account the
shardPlacementListlist obtained on the first step (in my case, there is only one table —dist_table, so there’s only one element in that list):-
Computation of the mean utilization (
totalCost/totalCapacity). In this example, the value is equal to671981568 / 2 = 335990784bytes. -
A limiting range in which a node is considered balanced is computed based on the
thresholdvalue. In my case it’s(302391712, 369589856), in bytes. -
Possible ways of shard placement are considered. This is the key part of the rebalancing algorithm. The main idea is moving shards from the more loaded shards onto the less loaded ones. Here, we will need both lists obtained on the step of sorting the list by node utilization/capacity. The algorithm is satisfied with the first acceptable movement that improves the cluster balance — it’s not looking for the best one (hence, it’s a greedy algorithm). If the current less loaded node isn’t fit, the algorithm moves to the next one. It finishes once there’s no way to improve the cluster balance. The limiting values are used to reach an acceptable balance and prevent the situations described above. This way:
-
From the obtained list (sorted in the descending order of utilization) we get the first element. It will be the node, from which we plan the movement, the so-called source node. In my case, it’s the
citus-db1node with two shards: 102490 and 102492 (their values in theshardidcolumn). -
If utilization of the source node is less than the left border of the (302391712, 369589856) limiting range, the algorithm considers the task as complete since there’s no point in moving shards from the less loaded nodes.
utilizationof the node in this case is 671416320 bytes, which is greater than the left border, so we move on. -
Otherwise, we start from the second node list that is sorted in the ascending order of utilization. Those will be the candidates for nodes that can be viewed as receivers of shards, the so-called receiver shards. In my case it’s the
citus-db2node with the utilization of 565248 bytes. -
If the utilization of the receiver shard is greater than the right border of the (302391712, 369589856) limiting range, there is no point in looking further, since there will only be nodes with the same or greater utilization. Also there is no point in other scenarios with limitations which will not be listed here. In this case the utilization is 565248 < 369589856 bytes.
-
For the chosen source and receiver nodes, we compute the predicted utilization after the movement (reduced at the source node, increased at the receiver node). First, we look at the 102492 shard with the cost of 417579008 bytes. If the movement occurs, the new load and utilization on the receiver node will be 418144256 bytes. For the source node — 253837312 bytes.
-
If after the possible movement the utilization of the receiver node becomes greater than the source node’s, the movement is considered profitable in terms of getting the cluster into a balanced state and the new cluster state can be update (for now, only in memory). In my case, the receiver node utilization would become greater (418144256 > 253837312), so the algorithm moves on.
-
If after the possible movement the utilization of the receiver node becomes greater than the source node’s before the movement, we need to decide whether this movement makes sense in terms of improving the general balance. The algorithm also checks the possible utilization improvement by the
improvement_threshold— if there is no profit in the movement, other movement options are considered. -
If a possible movement increases the cluster balance, the step is planned, in the memory state there’s an update of the cost and utilization, and the algorithm continues. Since the possible step improves the balance, the step of moving the 102492 shard with the cost of 417579008 bytes from the
citus-db1node to thecitus-db2node is planned. This is the first step that we see in the plan above. Next, the algorithm looks and the updated picture after the possible shard movement and considers thecitus-db2utilization as 418144256 bytes and moves on. -
If there are no possible steps to improve the balance, the algorithm stops.
-
-
-
After the algorithm’s finished, we can see what steps it chose to rebalance dist_table in my case:
select * from get_rebalance_table_shards_plan('dist_table'::regclass::oid);table_name | shardid | shard_size | sourcename | sourceport | targetname | targetport ------------+---------+------------+------------+------------+------------+------------ dist_table | 102492 | 417579008 | localhost | 8002 | localhost | 8003 dist_table | 102491 | 491520 | localhost | 8003 | localhost | 8002 dist_table | 102493 | 73728 | localhost | 8003 | localhost | 8002 (3 rows)
So, after the shard group movement, the cluster would be balanced as follows:
shardid | table_name | shard_size | shard_size_in_MiB | nodename | nodeport ---------+------------+------------+-------------------+-----------+---------- 102490 | dist_table | 253837312 | 242 | citus-db2 | 8003 102492 | dist_table | 417579008 | 398 | citus-db1 | 8002 102491 | dist_table | 491520 | 0 | citus-db1 | 8002 102493 | dist_table | 73728 | 0 | citus-db1 | 8002
Shard movement
On a high level, the shard movement looks like so: there are two types of movement — blocking, which blocks the operations with a shard until the movement is complete, and non-blocking (for the most part, since during the metadata update a block still occurs for some time) based on the logical replication.
Both types are based on creation of the new tables before the data is moved.
After the successful table shard movements, the sources are deleted.
If there are any errors, the completed operations remain as is.
The non-blocking type has an important detail in that if a distributed table has no primary key (or any unique index), the UPDATE and DELETE operations will fail. Which in a way makes it closer to a blocking type.
Listing the details of the movement can be an article of its own, so I will highlight the main points:
-
During the initial table creation on the receiver, the indexes and limitations are not created. The creation of these and several other objects occurs after the copying is finished and when the writing of fresh records is done.
-
The replication slot is created separately. When the subscription is created (
CREATE SUBSCRIPTION), the replication slot is not created (create_slot = false). That said, copying is carried out outside of the created subscription with the usage ofCOPY. Even though it can be done within the subscription (thecopy_dataparameter), it’s claimed that it is done with performance in mind, since among other methods binary copying can be used (also it seems that the internals of Adaptive Executor is used, which was discussed in the first part). -
Initially, the subscription is created in the
disabledmode, and turned on only after the copying. -
Before and after the creation of indexes, limitations, etc. there’s a wait for the new shard to catch up with the source LSN.
-
To update the table metadata, we have to wait for the DML operations to finish (to get a global block afterwards).
-
After we obtain a block, we wait for the writing of the fresh data.
-
Once it’s done, the metadata is updated (
pg_dist_placement). -
Also, it’s worth noting that "… final commit happens in a 2PC, with all the characteristics of a 2PC. If the commit phase fails on one of the nodes, writes on the shell table remain blocked on that node until the prepared transaction is recovered, after which they will see the updated placement. The data movement generally happens outside of the 2PC, so the 2PC failing on the target node does not necessarily prevent access to the shard".
If we compare this part of Citus with Greenplum, the differences are fundamental — for Greenplum the usage scenarios with data skew between segments are possible (it can’t resist it), but are rather scarce and point to a "poor" data distribution. For an even data distribution, it’s recommended to use certain practices. The saying "slowest camel sets the pace [of a caravan]" nicely highlights the possible problems that may arise because of the data skew. To control those system parameters, there are special views.
In general, the number of segments on each node is the same. In case of mirroring (which is obligatory for production use), in Greenplum there are 2 strategies of mirror placement: group and spread.
Thus, there is no rebalancing table data problem in Greenplum, since the scaling unit is a single PostgreSQL instance (a segment), which contains portions of data from all tables. However, a Greenplum cluster due to objective reasons (e.g. manual mirror movement, switching to mirrors, decommission and addition of new nodes) can get into an unbalanced state by a number of segments on each node (both primary and mirror segments). And that’s when a cluster needs to be rebalanced.
Here’s a quick spoiler: we plan to solve this problem in Greengage, more specifically, as a part of the ggshrink cluster problem.
Resource consumption control
It’s no secret that in Greenplum, the resource management is based on the resource groups (even in the earlier slot versions). Without that mechanism, it’s difficult to solve the problem of the resource distribution among many users with various levels of task importance. Obviously, such feature is a must-have for corporate users.
On one hand, Citus looks better in terms of resource utilization due to query multithreading in the form of division into subtasks that communicate with separate physical shards, but the lack of control can be detrimental with high-load clusters.
Comparison of TPC-DS test results
Formally, there is no TPC-DS test implementation for Citus (at least I couldn’t find any). The developers recommend using HammerDB. However, for OLAP it’s an implementation of the TPC-H specification. Furthermore, HammerDB doesn’t have an implementation for Greenplum.
Within the framework of this research, I wanted to compare the performance of Citus with Greenplum on the TPC-DS tests.
I had to partly adapt a test, that’s also suitable for Postgres.
With small edits I managed to adapt it for Citus as well. In particular, for Citus, I had to create the distributed and reference tables.
The creation of indexes, which in this PostgreSQL implementation is done for columns, I have left as is, even though it had significantly slowed down the data loading in comparison with Greenplum, where the schema defines only distribution keys and there are no indexes.
I had the following idea in mind — since Citus is declared to be a way to scale PostgreSQL, they approach to deployment of several instances and organization of a Citus cluster should be done with the same idea. The existence of indexes complies with it. Now we need to decide on the division between the distributed and reference tables and what keys to use to distribute data between shards. I took the division for these table types and distribution columns from the version suggested by the Citus developers for TPC-DS (it’s not a full implementation, but rather a set of scripts).
However, during the test launching, something interesting happened. For Citus, a calibrating test with a dataset of about 10 GB (in the implementation terms — scaling factor of 10) either didn’t finish in reasonable time, or was so slow that running it with a significant amount of data would be senseless. Out of pure interest, I ran such tests but cancelled them after a 3-hour timeout.
The implementation developers recommend using scaling factor of 3000 (i.e. around 3 TB), but considering the time it took to run the relatively fast test, I decided not to use such a dataset. To analyze the difference in execution time and to understand the reasons behind it, our dataset will suffice. Also I had to exclude 18 out of 99 queries that failed with such distribution columns. Nitpicking other columns and tailoring the queries for certain tests would probably ruin the functionality of other test, and I saw no pleasure in fixing the tests one after another.
Test stand configuration
Citus
| Node | Configuration |
|---|---|
citus coordinator node |
CPU(s): 32 |
citus worker node #1 |
CPU: 32 |
citus worker node #2 |
CPU: 32 |
Greenplum
| Node | Configuration |
|---|---|
master node |
CPU: 32 |
segment node #1 |
|
segment node #2 |
TPC-DS dataset
You can familiarize yourself with the data scheme and the TPC-DS specification here.
| Tablename | Citus table size (scale factor 100) | Citus table size (scale factor 10) | Citus table size (scale factor 1) | Greenplum table size (scale factor 100) |
|---|---|---|---|---|
call_center |
49 KB |
72 KB |
16 KB |
3,2 MB |
catalog_page |
10 MB |
6048 KB |
2 MB |
9 MB |
catalog_returns |
2,5 GB |
235 MB |
24 MB |
3,7 GB |
catalog_sales |
32 GB |
3 GB |
318 MB |
12,8 GB |
customer |
0,9 GB |
226 MB |
15 MB |
0,2 GB |
customer_address |
0,4 GB |
102 MB |
7 MB |
116 MB |
customer_demographics |
0,4 GB |
415 MB |
144 MB |
88 MB |
date_dim |
34 MB |
32 MB |
11 MB |
15 MB |
household_demographics |
1,22 MB |
1296 KB |
442 KB |
6,6 MB |
income_band |
24 KB |
24 KB |
8 KB |
6,5 MB |
inventory |
17 GB |
5,6 GB |
520 MB |
1,6 GB |
item |
0,2 GB |
95 MB |
6 MB |
63 MB |
promotion |
467 KB |
240 KB |
74 KB |
6,6 MB |
reason |
24 KB |
24 KB |
8 KB |
6,4 MB |
ship_mode |
24 KB |
24 KB |
8 KB |
6,4 MB |
store |
393 KB |
120 KB |
16 KB |
6,6 MB |
store_returns |
4,1 GB |
398 MB |
42 MB |
3,2 GB |
store_sales |
45 GB |
4,4 GB |
446 MB |
17,8 GB |
time_dim |
33 MB |
33 MB |
11 MB |
14 MB |
warehouse |
24 KB |
24 KB |
8 KB |
6,4 MB |
web_page |
762 KB |
96 KB |
8 KB |
6,6 MB |
web_returns |
1,1 GB |
105 MB |
11 MB |
0,9 GB |
web_sales |
15 GB |
1,4 GB |
153 MB |
6,6 GB |
web_site |
24 KB |
72 KB |
49 KB |
6,5 MB |
Comparison tests on the main set (scaling factor 100)
You can see the contents of each query here. Postfix in the test name matches the postfix of a template name. For example, the tpcds.01 test corresponds to the query1.tpl template.
| Test | Greenplum (scale factor 100) | Citus (scale factor 100) | Citus (scale factor 10) | Citus (scale factor 1) |
|---|---|---|---|---|
tpcds.01 |
00:00:01.131 |
— |
2h timeout |
00:02:38.158 |
tpcds.02 |
00:00:09.918 |
00:02:02.122 |
00:01:54.114 |
00:00:13.139 |
tpcds.03 |
00:00:00.864 |
00:00:00.433 |
00:00:00.605 |
00:00:00.125 |
tpcds.04 |
00:00:20.202 |
— |
2h timeout |
00:20:20.122 |
tpcds.05 |
00:00:02.258 |
— |
00:06:12.372 |
00:00:41.412 |
tpcds.06 |
00:00:00.561 |
00:00:11.119 |
00:00:13.130 |
00:00:01.104 |
tpcds.07 |
00:00:01.125 |
00:00:01.139 |
00:00:01.134 |
00:00:00.277 |
tpcds.08 |
00:00:00.739 |
00:00:00.591 |
00:00:00.526 |
00:00:00.628 |
tpcds.09 |
00:00:15.154 |
00:00:02.251 |
00:00:02.229 |
00:00:00.829 |
tpcds.10 |
00:00:01.128 |
not supported |
not supported |
not supported |
tpcds.11 |
00:00:10.101 |
— |
2h timeout |
00:05:09.309 |
tpcds.12 |
00:00:00.304 |
00:00:00.202 |
00:00:00.192 |
00:00:00.137 |
tpcds.13 |
00:00:02.241 |
00:00:00.466 |
00:00:00.476 |
00:00:00.164 |
tpcds.14 |
00:00:28.280 |
— |
00:07:13.433 |
00:00:48.485 |
tpcds.15 |
00:00:00.607 |
00:00:00.263 |
00:00:00.307 |
00:00:00.148 |
tpcds.16 |
00:00:07.734 |
not supported |
not supported |
not supported |
tpcds.17 |
00:00:02.221 |
00:00:00.380 |
00:00:00.360 |
00:00:00.202 |
tpcds.18 |
00:00:01.188 |
not supported |
not supported |
not supported |
tpcds.19 |
00:00:00.792 |
00:00:00.502 |
00:00:00.427 |
00:00:00.162 |
tpcds.20 |
00:00:00.362 |
00:00:00.223 |
00:00:00.245 |
00:00:00.125 |
tpcds.21 |
00:00:00.614 |
00:00:00.954 |
00:00:00.862 |
00:00:00.176 |
tpcds.22 |
00:00:06.633 |
not supported |
not supported |
not supported |
tpcds.23 |
00:01:10.702 |
— |
00:03:10.190 |
00:00:25.257 |
tpcds.24 |
00:00:18.185 |
00:00:13.137 |
00:00:12.127 |
00:00:00.19 |
tpcds.25 |
00:00:01.179 |
00:00:00.365 |
00:00:00.359 |
00:00:00.285 |
tpcds.26 |
00:00:01.102 |
00:00:00.944 |
00:00:00.764 |
00:00:00.232 |
tpcds.27 |
00:00:01.167 |
not supported |
not supported |
not supported |
tpcds.28 |
00:00:10.106 |
00:00:01.193 |
00:00:01.190 |
00:00:00.626 |
tpcds.29 |
00:00:03.336 |
00:00:00.295 |
00:00:00.295 |
00:00:00.236 |
tpcds.30 |
00:00:00.678 |
— |
00:26:48.160 |
00:00:09.911 |
tpcds.31 |
00:00:02.276 |
00:00:11.115 |
00:00:11.118 |
00:00:02.232 |
tpcds.32 |
00:00:00.776 |
not supported |
not supported |
not supported |
tpcds.33 |
00:00:01.137 |
00:00:00.57 |
00:00:00.549 |
00:00:00.303 |
tpcds.34 |
00:00:01.193 |
00:00:00.523 |
00:00:00.479 |
00:00:00.22 |
tpcds.35 |
00:00:02.245 |
not supported |
not supported |
not supported |
tpcds.36 |
00:00:04.428 |
not supported |
not supported |
not supported |
tpcds.37 |
00:00:02.236 |
not supported |
not supported |
not supported |
tpcds.38 |
00:00:05.526 |
00:00:14.146 |
00:00:14.146 |
00:00:02.207 |
tpcds.39 |
00:00:06.600 |
— |
00:02:31.151 |
00:00:16.167 |
tpcds.40 |
00:00:00.844 |
00:00:00.181 |
00:00:00.181 |
00:00:00.121 |
tpcds.41 |
00:00:00.161 |
00:00:09.989 |
00:00:10.103 |
00:00:00.527 |
tpcds.42 |
00:00:00.376 |
00:00:00.437 |
00:00:00.436 |
00:00:00.134 |
tpcds.43 |
00:00:02.219 |
00:00:00.477 |
00:00:00.434 |
00:00:00.165 |
tpcds.44 |
00:00:04.436 |
00:00:00.100 |
00:00:00.108 |
00:00:00.082 |
tpcds.45 |
00:00:00.721 |
00:00:00.288 |
00:00:00.272 |
00:00:00.142 |
tpcds.46 |
00:00:03.398 |
00:00:01.179 |
00:00:01.166 |
00:00:00.496 |
tpcds.47 |
00:00:05.524 |
— |
2h timeout |
00:37:12.223 |
tpcds.48 |
00:00:02.202 |
00:00:00.654 |
00:00:00.615 |
00:00:00.212 |
tpcds.49 |
00:00:01.140 |
00:00:00.311 |
00:00:00.284 |
00:00:00.178 |
tpcds.50 |
00:00:04.430 |
00:00:00.179 |
00:00:00.179 |
00:00:00.123 |
tpcds.51 |
00:00:08.894 |
00:00:25.256 |
00:00:26.261 |
00:00:03.339 |
tpcds.52 |
00:00:00.365 |
00:00:00.481 |
00:00:00.447 |
00:00:00.121 |
tpcds.53 |
00:00:01.132 |
00:00:01.108 |
00:00:01.105 |
00:00:00.174 |
tpcds.54 |
00:00:01.118 |
00:00:00.709 |
00:00:00.606 |
00:00:00.21 |
tpcds.55 |
00:00:00.414 |
00:00:00.411 |
00:00:00.377 |
00:00:00.134 |
tpcds.56 |
00:00:01.167 |
00:00:00.56 |
00:00:00.615 |
00:00:00.248 |
tpcds.57 |
00:00:03.300 |
— |
00:35:26.212 |
00:00:01.120 |
tpcds.58 |
00:00:01.104 |
00:00:00.839 |
00:00:00.848 |
00:00:00.326 |
tpcds.59 |
00:00:12.126 |
00:01:20.803 |
00:01:21.819 |
00:00:02.224 |
tpcds.60 |
00:00:01.192 |
00:00:00.847 |
00:00:00.761 |
00:00:00.349 |
tpcds.61 |
00:00:01.144 |
00:00:00.74 |
00:00:00.726 |
00:00:00.131 |
tpcds.62 |
00:00:02.273 |
00:00:00.352 |
00:00:00.32 |
00:00:00.197 |
tpcds.63 |
00:00:01.106 |
00:00:01.122 |
00:00:01.121 |
00:00:00.195 |
tpcds.64 |
00:00:11.116 |
00:01:11.712 |
00:01:16.766 |
00:00:01.125 |
tpcds.65 |
00:00:09.958 |
00:00:07.780 |
00:00:08.850 |
00:00:01.100 |
tpcds.66 |
00:00:01.160 |
00:00:00.438 |
00:00:00.497 |
00:00:00.291 |
tpcds.67 |
00:01:41.101 |
not supported |
not supported |
not supported |
tpcds.68 |
00:00:02.230 |
00:00:00.664 |
00:00:00.651 |
00:00:00.245 |
tpcds.69 |
00:00:01.161 |
not supported |
not supported |
not supported |
tpcds.70 |
00:00:04.495 |
not supported |
not supported |
not supported |
tpcds.71 |
00:00:01.105 |
00:00:00.647 |
00:00:00.644 |
00:00:00.218 |
tpcds.72 |
00:00:26.267 |
00:00:00.766 |
00:00:00.790 |
00:00:00.972 |
tpcds.73 |
00:00:01.107 |
00:00:00.351 |
00:00:00.371 |
00:00:00.208 |
tpcds.74 |
00:00:06.679 |
— |
2h timeout |
00:01:54.114 |
tpcds.75 |
00:00:05.583 |
00:00:39.398 |
00:00:39.399 |
00:00:04.477 |
tpcds.76 |
00:00:03.351 |
00:00:04.490 |
00:00:05.534 |
00:00:00.815 |
tpcds.77 |
00:00:01.145 |
not supported |
not supported |
not supported |
tpcds.78 |
00:00:18.180 |
00:01:18.786 |
00:01:17.777 |
00:00:08.890 |
tpcds.79 |
00:00:05.523 |
00:00:01.188 |
00:00:01.182 |
00:00:00.449 |
tpcds.80 |
00:00:02.244 |
00:00:01.177 |
00:00:01.155 |
00:00:00.738 |
tpcds.81 |
00:00:00.977 |
— |
01:50:21.662 |
00:00:07.747 |
tpcds.82 |
00:00:09.908 |
not supported |
not supported |
not supported |
tpcds.83 |
00:00:01.106 |
00:00:00.576 |
00:00:00.606 |
00:00:00.338 |
tpcds.84 |
00:00:00.619 |
00:00:00.188 |
00:00:00.199 |
00:00:00.122 |
tpcds.85 |
00:00:02.208 |
00:00:00.279 |
00:00:00.298 |
00:00:00.191 |
tpcds.86 |
00:00:01.112 |
not supported |
not supported |
not supported |
tpcds.87 |
00:00:05.542 |
00:00:15.151 |
00:00:15.154 |
00:00:02.211 |
tpcds.88 |
00:00:14.144 |
00:00:01.191 |
00:00:02.209 |
00:00:00.606 |
tpcds.89 |
00:00:01.114 |
00:00:01.120 |
00:00:01.120 |
00:00:00.197 |
tpcds.90 |
00:00:01.167 |
00:00:00.289 |
00:00:00.289 |
00:00:00.112 |
tpcds.91 |
00:00:00.698 |
00:00:00.159 |
00:00:00.151 |
00:00:00.127 |
tpcds.92 |
00:00:00.611 |
not supported |
not supported |
not supported |
tpcds.93 |
00:00:04.465 |
00:00:00.197 |
00:00:00.220 |
00:00:00.102 |
tpcds.94 |
00:00:03.314 |
not supported |
not supported |
not supported |
tpcds.95 |
00:00:23.236 |
not supported |
not supported |
not supported |
tpcds.96 |
00:00:03.327 |
00:00:00.352 |
00:00:00.341 |
00:00:00.131 |
tpcds.97 |
00:00:07.708 |
00:00:00.825 |
00:00:00.638 |
00:00:00.195 |
tpcds.98 |
00:00:00.673 |
00:00:00.472 |
00:00:00.417 |
00:00:00.168 |
tpcds.99 |
00:00:03.344 |
00:00:00.764 |
00:00:00.476 |
00:00:00.178 |
I suggest discussing one test, which saw a large time difference and which I had to stop with a timeout:
| Test | Greenplum (scale factor 100) | Citus (scale factor 100) | Citus (scale factor 10) | Citus (scale factor 1) |
|---|---|---|---|---|
tpcds.01 |
00:00:01.131 |
— |
2h timeout |
00:02:38.158 |
The query itself:
WITH customer_total_return AS
(
SELECT
sr_customer_sk AS ctr_customer_sk,
sr_store_sk AS ctr_store_sk,
SUM(SR_RETURN_AMT_INC_TAX) AS ctr_total_return
FROM store_returns, date_dim
WHERE
sr_returned_date_sk = d_date_sk AND d_year = 1999
GROUP BY sr_customer_sk, sr_store_sk
)
SELECT c_customer_id
FROM customer_total_return ctr1, store, customer
WHERE ctr1.ctr_total_return > (SELECT avg(ctr_total_return) * 1.2
FROM customer_total_return ctr2
WHERE ctr1.ctr_store_sk = ctr2.ctr_store_sk)
AND s_store_sk = ctr1.ctr_store_sk
AND s_state = 'TN'
AND ctr1.ctr_customer_sk = c_customer_sk
ORDER BY c_customer_id
LIMIT 100;The special thing about this query is in the nested related subquery.
For each row in the customer_table_return table expression, we have to decide if the ctr_total_return value for the customer-store pair (sr_customer_sk and sr_store_sk) is greater than the average value for the store plus 20%.
This way, by brute force we can iterate over the set of the computed ctr_total_return expression and comparing the ctr_total_return attribute with the result of the SUM aggregating function for that store.
Looking at the Citus plan, we can that’s exactly what it does.
The EXPLAIN plan for Citus:
QUERY PLAN
-------------------------------------------------------------------------------------------------------------------------
Custom Scan (Citus Adaptive)
-> Distributed Subplan 62_1 (1)
-> HashAggregate
Group Key: remote_scan.ctr_customer_sk, remote_scan.ctr_store_sk
-> Custom Scan (Citus Adaptive)
Task Count: 32 (2)
Tasks Shown: One of 32
-> Task
Node: host=localhost port=8002 dbname=postgres
-> GroupAggregate
Group Key: store_returns.sr_customer_sk, store_returns.sr_store_sk
-> Sort
Sort Key: store_returns.sr_customer_sk, store_returns.sr_store_sk
-> Nested Loop (3)
-> Seq Scan on store_returns_102358 store_returns
-> Memoize
Cache Key: store_returns.sr_returned_date_sk
Cache Mode: logical
-> Index Scan using date_dim_pkey_102318 on date_dim_102318 date_dim (4)
Index Cond: (d_date_sk = store_returns.sr_returned_date_sk)
Filter: (d_year = 1999)
Task Count: 1
Tasks Shown: All
-> Task
Node: host=localhost port=8000 dbname=postgres
-> Limit
-> Sort
Sort Key: customer.c_customer_id
-> Nested Loop
-> Nested Loop
Join Filter: (intermediate_result.ctr_store_sk = store.s_store_sk)
-> Function Scan on read_intermediate_result intermediate_result
Filter: (ctr_total_return > (SubPlan 1))
SubPlan 1
-> Aggregate
-> Function Scan on read_intermediate_result intermediate_result_1
Filter: (intermediate_result.ctr_store_sk = ctr_store_sk)
-> Materialize
-> Seq Scan on store_102357 store
Filter: ((s_state)::text = 'TN'::text)
-> Index Scan using customer_pkey_102315 on customer_102315 customer
Index Cond: (c_customer_sk = intermediate_result.ctr_customer_sk)As we see from the plan, Citus decided to format the customer_total_return table expression as a distributed subplan (marker 1).
Internally, the plan was distributed across 32 tasks since the default number of shards for the store_returns table is 32 (marker 2).
The choice of the Nested Loop join (marker 3) is probably correct in this case, since the given TPC-DS implementation builds indexes by certain fields and such index was chosen for the join with date_dim (marker 4).
The execution of this subplan led to a creation of a temporary file which was already used in the main query, which was executed on the coordinator. For this query, we have to run a correlated nested query:
where ctr1.ctr_total_return > (select avg(ctr_total_return) * 1.2
from customer_total_return ctr2
where ctr1.ctr_store_sk = ctr2.ctr_store_sk)This part corresponds to the following EXPLAIN execution plan:
-> Nested Loop (cost=0.29..12733.24 rows=20 width=17)
-> Nested Loop (cost=0.00..12603.32 rows=20 width=4) (1)
Join Filter: (intermediate_result.ctr_store_sk = store.s_store_sk)
-> Function Scan on read_intermediate_result intermediate_result (cost=0.00..12542.50 rows=333 width=8) (2)
Filter: (ctr_total_return > (SubPlan 1))
SubPlan 1
-> Aggregate (cost=12.52..12.53 rows=1 width=32)
-> Function Scan on read_intermediate_result intermediate_result_1 (cost=0.00..12.50 rows=5 width=32)
Filter: (intermediate_result.ctr_store_sk = ctr_store_sk)And the actual EXPLAIN ANALYZE:
-> Materialize (cost=0.00..50601517.68 rows=20 width=4) (actual time=0.031..154.745 rows=12734 loops=665)
-> Nested Loop (cost=0.00..50601517.58 rows=20 width=4) (actual time=20.473..102683.089 rows=12753 loops=1) (1)
Join Filter: (intermediate_result.ctr_store_sk = store.s_store_sk)
Rows Removed by Join Filter: 55645
-> Function Scan on read_intermediate_result intermediate_result (cost=0.00..50587820.49 rows=76412 width=8) (actual time=20.458..102674
.660 rows=12753 loops=1)
Filter: (ctr_total_return > (SubPlan 1))
Rows Removed by Filter: 37009
SubPlan 1
-> Aggregate (cost=662.02..662.03 rows=1 width=32) (actual time=2.063..2.063 rows=1 loops=49762) (2)
-> Function Scan on read_intermediate_result intermediate_result_1 (cost=0.00..570.65 rows=36545 width=32) (actual time=0.013..1.566 rows=8123 loops=49762) (3)
Filter: (intermediate_result.ctr_store_sk = ctr_store_sk) (4)
Rows Removed by Filter: 41639
-> Materialize (cost=0.00..1.21 rows=12 width=4) (actual time=0.000..0.000 rows=5 loops=12753)
-> Seq Scan on store_102357 store (cost=0.00..1.15 rows=12 width=4) (actual time=0.009..0.012 rows=10 loops=1)
Filter: ((s_state)::text = 'TN'::text)As we can see, the planner had to make a decision with a faulty input data.
With other options missing (since the estimation is used for read_intermediate_result), the Function Scan on read_intermediate_result intermediate_result node estimated that it would return 333 rows (marker 2 in the EXPLAIN output).
In fact, according to EXPLAIN ANALYZE, the actual number of rows is one order of magnitude greater (marker 3 in the EXPLAIN ANALYZE output). For a different scale factor, the error will be greater.
The slowest part of this plan, according to the subplan execution, is Nested Loop (marker 1). For each row of the intermediate result, an aggregating function is called (marker 2) to compute SUM for the given ctr_store_sk (marker 4). Doesn’t look very optimal.
Greenplum and GPORCA, as it seems to me, build a more advanced plan which leads to such a significant time difference:
QUERY PLAN
-------------------------------------------------------------------------------------------------------------------------
Gather Motion 2:1 (slice9; segments: 2)
Merge Key: customer.c_customer_id
-> Sort
Sort Key: customer.c_customer_id
-> Sequence
-> Shared Scan (share slice:id 9:0) (1)
-> Materialize
-> HashAggregate
Group Key: store_returns.sr_customer_sk, store_returns.sr_store_sk
-> Redistribute Motion 2:2 (slice8; segments: 2) (2)
Hash Key: store_returns.sr_customer_sk, store_returns.sr_store_sk
-> Hash Join
Hash Cond: (store_returns.sr_returned_date_sk = date_dim.d_date_sk)
-> Dynamic Seq Scan on store_returns (dynamic scan id: 1)
-> Hash
-> Partition Selector for store_returns (dynamic scan id: 1)
-> Broadcast Motion 2:2 (slice7; segments: 2) (3)
-> Seq Scan on date_dim
Filter: (d_year = 1999)
-> Redistribute Motion 1:2 (slice6)
-> Limit
-> Gather Motion 2:1 (slice5; segments: 2)
Merge Key: customer.c_customer_id
-> Limit
-> Sort
Sort Key: customer.c_customer_id
-> Hash Join
Hash Cond: (customer.c_customer_sk = share0_ref3.sr_customer_sk)
-> Seq Scan on customer
-> Hash
-> Redistribute Motion 2:2 (slice4; segments: 2)
Hash Key: share0_ref3.sr_customer_sk
-> Hash Join
Hash Cond: (share0_ref3.sr_store_sk = store.s_store_sk)
-> Hash Join
Hash Cond: (share0_ref3.sr_store_sk = share0_ref2.sr_store_sk)
Join Filter: (share0_ref3.ctr_total_return > (((pg_catalog.avg((avg(share0_ref2.ctr_total_return
)))) * 1.2))) (4)
-> Shared Scan (share slice:id 4:0)
-> Hash
-> Broadcast Motion 2:2 (slice2; segments: 2) (5)
-> Result
-> Result
-> HashAggregate
Group Key: hare0_ref2.sr_store_sk
-> Redistribute Motion 2:2 (slice1; segments: 2)
Hash Key: share0_ref2.sr_store_sk
-> Result
-> HashAggregate (6)
Group Key: share0_ref2.sr_store_sk
-> Shared Scan (share slice:id 1:0)
-> Hash
-> Broadcast Motion 2:2 (slice3; segments: 2)
-> Seq Scan on store
Filter: ((s_state)::text = 'TN'::text)
Optimizer: Pivotal Optimizer (GPORCA)Comparing two plans, we can note that the distributed, paralleled part of the Citus plan can be matched with Shared Scan (marker 1).
In fact, it’s the same action and result in terms of data.
In this implementation of TPC-DS, Greenplum has no indexes, all tables are DISTRIBUTED BY, so the date_dim table has to be redistributed with Broadcast Motion to all the segments (marker 2). Then, the store_returns table is joined with date_dim, aggregated by the sr_customer_sk and sr_store_sk columns, and redistributed between segments by these two columns (marker 3).
The key difference is how Greenplum processes the nested correlated subquery.
First, there’s a grouping by the sr_store_sk field and precomputation of the SUM (marker 6).
Second, this set of rows is redistributed by Broadcast Motion by the sr_store_sk attribute (marker 5).
It allows us to perform Hash Join of the original set from Shared Scan with a precomputed set by the sr_store_sk column, and this way just apply the Join Filter condition to ctr_total_return taking into account the avg(ctr_total_return) * 1.2 expression (marker 4).
This step allows us to execute the query several orders of magnitude quicker. Citus computes the aggregate of the nested correlated query for each row form the inner set for the Nested Loop join.
Greenplum has computed everything and just runs Hash Join with the same condition.
Out of interest, I looked at the detailing of the first query. Here we can see where Citus spends most of the time.
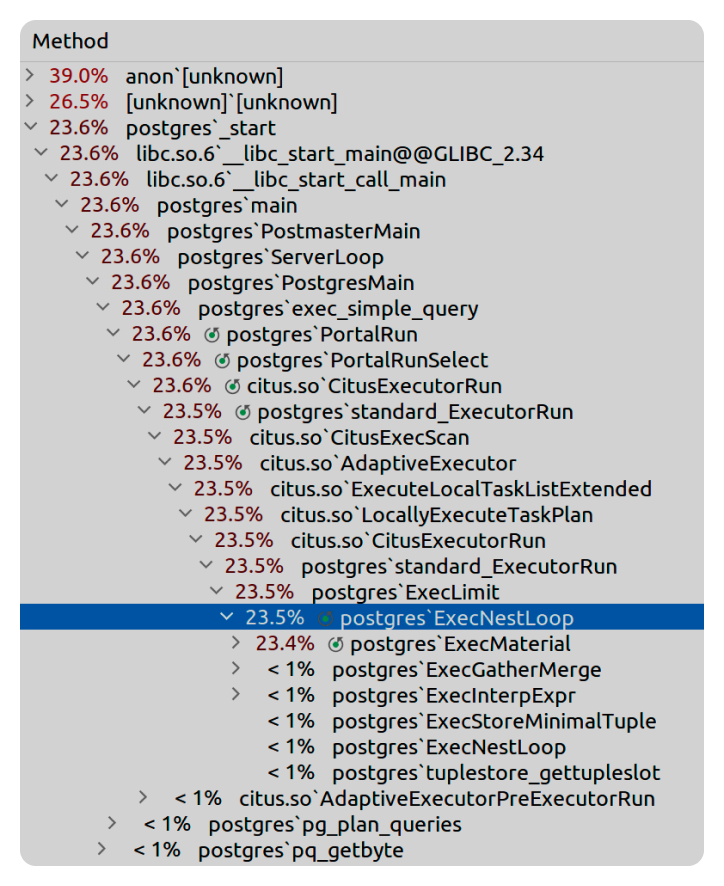
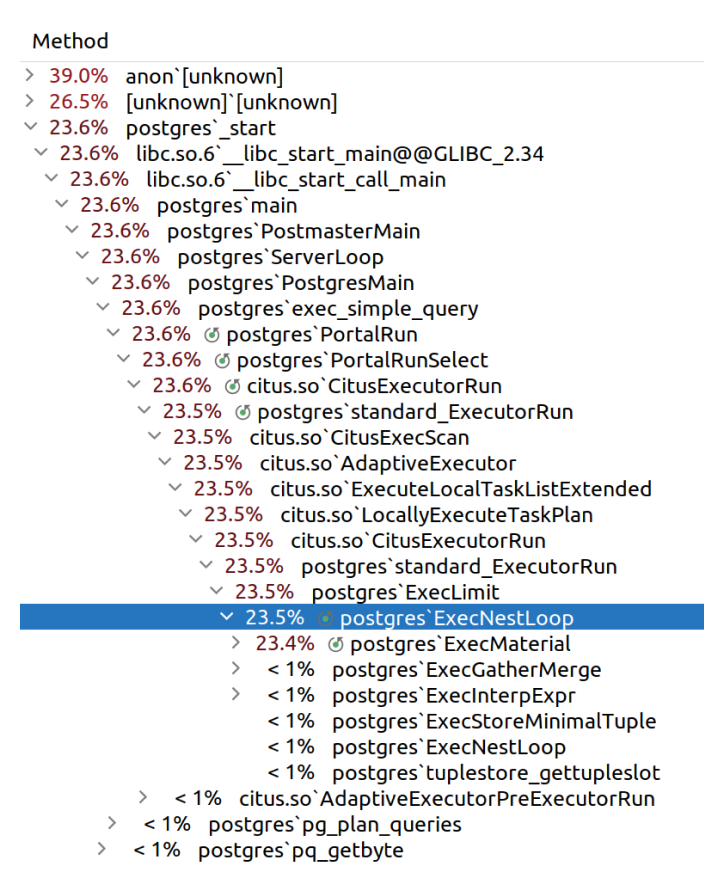
Results
I made the following conclusions for myself:
-
Using Citus for OLAP and ad-hoc queries may be problematic. With complex data queries, it will be extremely difficult to adjust co-located columns to each query; we will leave the convenience issue out of the equation. Some might say that executing such queries isn’t the main task for Citus and is included as a bonus, but there are possibilities, the planner has support for it, and the developers have worked on that feature.
-
The Greenplum planner handles complex OLAP queries better.
-
Using finely partitioned tables in Citus, in my opinion, is a "bomb" that can explode as the number of tables in the database increases. Remember that for each leaf partition, 32 shard tables are created by default. Some might create more, which will only worsen the situation with the number of tables.
-
It’s easier to scale Citus, a node can be decommissioned with a single API request.
-
It’s a great option for the problem of horizontally scaling an existing PostgreSQL cluster.
-
There are no particular difficulties with deployment of a small Citus cluster; however, for larger systems, there are no possibilities of an automatic cluster deployment. Greenplum has at least
gpinitsystemfor manual deployments. -
The rebalance strategies considered here allow supporting a wider range of usage scenarios which Greenplum isn’t focused on.
-
An interesting Citus feature is an ability to connect to worker nodes and run queries directly from them. This way, any node can be viewed as a coordinator. Currently, there are some restrictions — you can’t run queries that change the cluster state (DDL queries,
create_distributed_table, etc.). In such cases, we have to run a query on a dedicated coordinator. -
When working with Citus, it’s important to remember that distributed snapshots are not supported; hence there are no guarantees of the visibility rules compliance for the committed transactions within the whole cluster.